Кафедра Физики Высоких Энергий и Элементарных Частиц

Из переписки В. А. Фока
с Шредингером и Дираком

Шредингер — Фоку

Берлин-Грюневальд,
Куноштрассе, 44.
11 мая 1931 г.

Дорогой господин Фок!
Большое спасибо за Ваше дружеское письмо от 30 апреля. Оператор $H/|H|=\rho$ есть непосредственно тот, который мне сообщил господин фон Нейман и который с помощью преобразований каждое переводит в :

$\rho^{-1}(g+U)\rho=g-U; \rho^{-1}\equiv \rho.$

(Сравните замечание в последнем пункте моей статьи от 29 января 1931 г.) Прямо отсюда, так как система всех полностью эквивалентна системе всех , я полагаю, что ни одна из них не является правильной, но что, например, операторы, названные $\tilde{x}_k$ , соответствуют координатам электронов. ( Когда я, кроме того, в следующем пункте подразумеваю, что, возможно, лоренцевы преобразования имеют место для собственных значений $\tilde{x}_k$ и , то здесь содержится ошибка, так как $\tilde{x}_k$ не коммутируют. Их коммутаторы весьма интересны, по существу, представляют собой четную часть спина.
Ваше возражение ("квадрат оператора", "оператор квадрата") я не считаю серьезным. Нами определена только пара основных операторов. Если перейти от , к $\tilde{x}_k$ , то это коснется больше $\tilde{x}_k^2$ — по крайней мере в принципе.
Я был удивлен, что Вы соглашаетесь с точностью моей оценки порядков величин только теперь, а не выводите ее просто исходя из используемого нами метода. Если за этим кроется ошибка, мне было бы очень приятно ее узнать.
Прилагаемую не очень важную статью я посылаю на днях господину Шеелю (Карл Шеель — издатель журнала "Zeitschrift ur Physik"). Надеюсь, Вы не сомневаетесь в том, что она действительно не подразумевается как полемическая, я поступил так только лишь для пользы дела, чтобы тот, кто интересуется вопросом, мог изучить достаточно простой метод расчета. При этом неизбежно в последнем абзаце развил свою точку зрения на усреднение по времени. Впрочем, я надеюсь, что Вы по существу будете иметь со мной одну точку зрения.
На веселое "Ну!" я больше не отзываюсь. Я не думаю, что Вы с Вашей "необходимостью" правы. Со своей стороны я только сказал, что невзирая на Ваши возражения, мне "хотелось бы твердо держаться" своих (потому что мне симпатична эта точка зрения). Так как два понятия, которые в теории Лоренца представляются просто как одно, в теории Дирака расщепляются, то, в сущности, довольно очевидно, что с точки зрения принципа соответствия их операторное описание содержит некоторый произвол.

Примите наилучшие пожелания от искренне преданного Вам
Э. Шредингера.

(С.-Пб. отд. арх. РАН. Ф.1034, ед.хр. 772, л.2.)

Фок — Шредингеру

22 мая
(Год здесь не указан. Но, очевидно, что это 1931 год.)

Дорогой господин Шредингер!
Большое спасибо за Ваше дружеское письмо от 11 мая и присылку рукописи.
Ваша статья содержит для меня так много интересного, что я под впечатлением Вашей "Квантовой динамики электрона" хотел написать нечто подобное; но я не сделал этого.
Почему Вы ничего не пишете там об операторе $\rho=H/|H|$ , Ведь он представляет простое и единственное среднее при вычислении четных частей операторов! Было бы очень жаль, если бы это осталось неотмеченным.
В Вашем "Замечании" (E.Schrodinger. Замечания к работе г. Фока "Внутренние степени свободы электрона". Zs.f.Phys., В.70, Н.11/12, S.808.) Вы не сказали ничего о магнитном поле. Мне кажется, что различие между свободным и несвободным случаями заслуживает внимания. Далее, я не могу как следует понять, почему "усреднение по времени в смысле Фока" не является обычным усреднением. Мои соображения по этому поводу я изложил в прилагаемой маленькой заметке. Я хотел бы просить Вас мою заметку переслать г. Шеелю для того, чтобы она появилась в журнале вместе с Вашими "Замечаниями". Но если Вы сделали в своей статье изменения, которые учитывают мои замечания, я хотел бы предоставить Вам решение вопроса, имеет ли еще смысл публиковать мою заметку.
Об операторе для квадрата я хотел бы заметить следующее. Если $\rho=H/|H|$ , то Вы определяете оператор для x как g и для x² как g². Но это g² не является четной частью, так как

$x^2=(g^2+x^2)+(Ug+gU)\equiv g^{\prime}+U^{\prime}$

А затем примем основной оператор в указанном выше смысле; возникает произвол: почему в качестве основного оператора следует выбирать x, а не f(x)?
Кроме того, при Вашем определении действия с операторами будут безнадежно сложными. Как вычислите Вы, например, $\frac{1}{\sqrt{\tilde{x}^2+\tilde{y}^2+\tilde{z}^2}}$ ? Четная часть от 1/r наименее представима в указанной форме в p-пространстве.

С множеством дружеских приветов
сердечно преданный Вам

В. Фок.

(С.-Пб. отд. арх. РАН. Ф.1034, оп.3, ед.хр.195, л.4.)

Дирак — Фоку

Кембридж,
9 ноября 1930 г.

Дорогой Фок,
теория фотонов, набросок которой Вы дали в Вашем письме ко мне от 27 сентября ( В статье "La mecanique des photons" (Compt. Rend. 1930. Т. 190. Р. 1399-1401) Фок предложил волновое уравнение для фотона, связав его с уравнениями Максвелла. В упомянутом письме от 27 сентября он пишет Дираку о дальнейшем развитии своей теории и о выводе, что координата фотона не является наблюдаемой.
Об этой теории Фока см.: Кожевников А. Б. В. А. Фок и метод вторичного квантования // Исследования по истории физики и механики, 1988.

В. А. Фок и П. А. М. Дирак
Ленинград, 1973 г.
М.: Наука, 1988. С. 315-338. Там же опубликованы два письма Фока Дираку от 27.09.1930 г. и 18.11.1930 г.), представляется вполне самосогласованной и не вызывающей возражений, но я думаю, что это не единственная возможная удовлетворительная теория фотонов. Пока мы рассматриваем только фотоны сами по себе и пренебрегаем их взаимодействием с материей, мы будем знать о них так мало, что, думается, окажется возможным построить много теорий, которые в равной мере были бы удовлетворительными. Я не считаю, что волновая функция фотона совершенно определенно должна удовлетворять уравнениям Максвелла, потому что если бы это было так, то она должна была бы быть нормирована относительно энергии, тогда как все другие волновые функции в квантовой механике нормированы относительно числа частиц. Я думаю, что в настоящее время нельзя сказать ничего определенного о волновой функции фотона. Нужно иметь теорию, которая учитывает взаимодействие фотонов с материей, прежде чем можно будет решить, правильно это или нет.
Я недавно был в Брюсселе на Сольвеевском конгрессе ( Шестой Сольвеевский конгресс проходил с 20 по 25 октября 1930 г.), встретил там великое множество физиков и хорошо провел время.

С наилучшими пожеланиями
искренне Ваш

П. А. М. Дирак

Фок — Дираку

Ленинград,
7 июля 1932 г.

Дорогой Дирак!
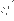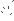Большое спасибо за оттиск Вашей "Релятивистской квантовой механики". Я изучил ее с огромным интересом. Я рассчитал (вместе с Б. Подольским из Харькова) трехмерный случай и получил в первом приближении (пренебрегая всеми релятивистскими поправками) кулоновское взаимодействие с правильным знаком. Но есть еще и лишние члены, а именно бесконечные константы, умноженные на $\varepsilon_1^2$ и $\varepsilon_2^2$ . Я рассчитал также случай с Вашим волновым уравнением для электрона. Я надеялся получить что-то вроде уравнения Брейта для двух электронов. Я нашел, что если пренебречь запаздыванием (чего, правда, в этом случае делать нельзя), то получаются кажущиеся разумными члены взаимодействия, а именно кулоновская сила из скалярного потенциала и члены:

(в единицах Хевисайда) из векторного потенциала.
Но запаздывание, кажется, получается в неправильной форме. Кроме этого, есть еще нежелательные мнимые и логарифмические члены. Тем не менее я думаю, что идея Вашей работы имеет фундаментальное значение, и надеюсь, что с некоторыми поправками теория станет правильной.
Я очень рад, что Вы намереваетесь приехать в Ленинград в сентябре!

С дружеским приветом

Ваш В. Фок

Дирак — Фоку

Кембридж,
19 июля 1932 г.

Дорогой Фок,
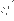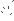большое спасибо за Ваше письмо. Можно было ожидать, что члены с $\varepsilon_1^2$ и $\varepsilon_2^2$ . войдут также и в трехмерный случай, потому что они встречаются в одномерном случае, хотя я и опустил их в своей статье. Розенфельд из Копенгагена сделал некую работу (еще не опубликованную), которая, вроде бы, показывает, что моя новая работа математически эквивалентна теории Гейзенберга-Паули для волновых уравнений, линейных относительно $\partial /\partial t$ .
Ваши перестановочные соотношения для потенциалов являются, я думаю, такими же, как соотношения Ферми. Сложность с этой схемой состоит в условии $(1/c) \dot Q_0+{\rm div\,} Q=0$ .
Если имеем $\psi=\psi_0+\varepsilon\psi_1+\varepsilon^2\psi_2+\dots$ то можно условиться, что $((1/c) \dot Q_0+{\rm div\,} Q)\psi_0=0$ но тогда в общем случае не получится

$[(1/c) \dot Q_0+{\rm div\,} Q]\psi_1=0$ (не так ли?)

так что я не вижу, как Вы использовали это условие в Ваших вычислениях. Я был бы рад, если бы Вы смогли рассказать мне определенно, что Вы делаете с этим условием. Надеюсь встретить Вас в сентябре.

Искренне Ваш

П. А. М. Дирак

Письмо вебмастеру

Февраль 2004